Chemistry is all about how elements combine and react with one-another. Given the large number of elements, and the even larger number of combinations, it should come as no surprise that there is a lot of complicated phenomonology in chemistry. We will not be able to understanding all of it -- merely laying down the basic physical foundations of chemistry.

Chemical Bonds

As a concrete place to begin understanding chemical bonds, lets think a bit about ionized molecular hydrogen $H_2^+$. We will start with this strange species merely because it is simple. From it we will gain confidence.

We have two protons and one electrons. Nominally we want to solve a Schrodinger equation in 9 variables, for a wavefunction $\Psi(R_1,R_2,r)$,
\begin{eqnarray}
H\Psi&=&E\Psi
\label{ham}\\\nonumber
H&=&-\frac{\nabla_{R_1}^2}{2 M_p}-\frac{\nabla_{R_2}^2}{2 M_p}-\frac{\nabla_{r}^2}{2 m_e}% \\\nonumber&&
-\frac{e^2}{4\pi\epsilon_0}\left[\frac{1}{|R_1-r|}+
\frac{1}{|R_2-r|}
- \frac{1}{|R_1-R_2|}\right].
\end{eqnarray}
Wow. Even with the help of a computer, how are we ever going to find the eigenvectors/eigenvalues?

Taking a cue from the dimensional analysis lecture, we should write down all of the dimensionless variables in the problem. One simplifying principle is that if any of the dimensionless variables are really small, you either know they drop out, or they are going to enter in some simple way. Here we have a small number $m_e/M_p\sim5\times10^{-4}$: the
The protons are a lot heavier than the electron. Physically this means they move slower. Lets take this to the extreme. Suppose the protons are stuck at positions $\bf R_1$ and $\bf R_2$. The electron will then obey a Schrodinger equation
\begin{equation}\label{born}
E\psi({\bf r})= \left[-\frac{\nabla_{r}^2}{2 m_e}-V(r)\right]\psi({\bf r}),
\end{equation}
where
\begin{equation}
V({\bf r})=-\frac{e^2}{4\pi\epsilon_0}\left[\frac{1}{|R_1-r|}+\frac{1}{|R_2-r|} - \frac{1}{|R_1-R_2|}\right].
\end{equation}
Great! This we can handle. Its just a single particle Schrodinger equation in a double-well potential. We know how to numerically solve it.

We have a problem though: The solution depends on $R_1-R_2$. That is the energy in Eq.~\ref{born} should be written $E(R_1,R_2)$, and the wave-function should be
$\psi_{R_1R_2}(r)$. How do we choose the separation between the protons?

The answer is we choose $R_1$ and $R_2$ to minimize the energy. Our approximation is actually a variational ansatz:
\begin{equation}
\Psi(R_1,R_2,r)=\delta (R_1-R_1^*)\delta(R_2-R_2^*)\psi_{R_1R_2}(r),
\end{equation}
and it turns out that the $E(R_1^*,R_2^*)$ that we wrote down is just the expectation value of the Hamiltonian in this state.

Qualitative picture of energy surface

When $R_1^*$ and $R_2^*$ are far apart, you essentially have two independent protons, and one electron. The ground state should be two-fold degenerate: The energy is the same regardless of which proton the electron is on. As you bring the protons closer together, the electron can tunnel from one proton to the other. This splits the ground state. The symmetric state goes down in energy, while the antisymmetric state goes up. As the protons get closer the symmetric one keeps getting lower, and the antisymmetric one keeps getting higher. Eventually the Coulomb repulsion between the protons becomes significant, and both potential curves rise. This gives a potential which looks like:

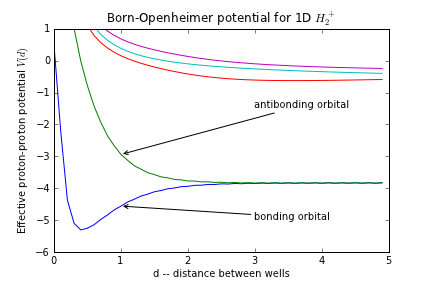
The symmetric state has an energy minimum at some finite radius: it is called a "bonding orbital." If the electron is in this state it pulls the protons together. On the other hand the antisymmetric state has no energy minimum, and if the electron is in this state it pushes the protons apart. This is an "antibonding" orbital.

Hydrogen can form a diatomic molecule, since the first two electrons will go into the bonding orbitals. Helium, however does not form a diatomic molecule. We put 4 electrons in the system: 2 end up in bonding orbitals and 2 in antibonding. The net result is a repulsion.

Born-Openheimer

For a lot of physics/chemistry, this variational approach suffices. I feel obliged to discuss a slightly more sophisticated approximation -- the Born-Openheimer approximation.

Born and Openheimer noted that once you have the potential that the nuclei feel, you can solve the quantum mechanical problem:
\begin{equation}
-\frac{\nabla^2}{2\mu} \Psi_N({\bf R})+V_{\rm eff}(R) \Psi_N({\bf R})=E \Psi_N({\bf R})
\end{equation}
where $\bf R=R_1-R_2$ is the separation between the nuclei, $\mu^{-1}=2 M_p^{-1}$ is the reduced mass for the nuclear system, and
\begin{equation}
V_{\rm eff}(R)= E(R/2,-R/2)
\end{equation}
is the energy of two nuclei separated by a distance $R$. The Born=Openheimer approximation is almost variational -- it is what you would find if you took the wavefunction
\begin{equation}
\Psi(R_1,R_2,r)=\Psi_N(R_1-R_2)\psi_{R_1R_2}(r),
\end{equation}
then neglected terms which are higher than first order in $m_e/M_p$.

Asymptotics of chemical bonds

The bond in $H_2^+$ was particularly simple, but is a covalent bond -- neutral $H_2$ will have a similar bond . Unfortunately, the interaction between the electrons makes it more complicated to calculate the inter-atomic potential. Rather than going through a lengthy calculation, many chemists just write down a broad functional form, then fit parameters to experimental measurements. A typical empirical form is
\begin{equation}
V=-\frac{A}{r^n}+\frac{B}{r^m},
\end{equation}
with $m>n$. Probably the most popular potential of this form is the ``6-12" potential, where $n=6$ and $m=12$. The 12 was pretty arbitrary, but the 6 is chosen to match the correct asymptotic behavior of the potential. The $r^{-6}$ tail was first studied by Van der Waals, who argued based on a picture of fluctuating dipoles. Complete the Van der Waals activity to derive this.

The coefficient of the Van der Waals force is going to be strongest between two molecules with permanent electric dipole moments (such as H$_2$O or CO), and weakest between to molecules with no moments.

Simplifications

Even with Born-Openheimer, it can be hard to calculate the properties of a molecule formed from multi-electron atoms. There are a number of numerical techniques which go beyond what we want to do in this class (Density Functional Theory, Configuration Interaction,..). I was reading Pauling's book on the Chemical bond, and he uses a simple variational wavefunction which seems worth mentioning. For the $H_2^+$ molecular ion, he took the positions of the nuclei to be fixed, and wrote
\begin{equation}
\psi_{R_1,R_2}({\bf r})=A \psi_0(|r-R_1|)+B \psi_0(|r-R_2|),
\end{equation}
where $\psi_0$ is just the $1s$ wavefunction of Hydrogen.
that is you just take the electron wavefunction to be the weighted sum of the two $1s$ orbits. The energy is minimized when $A=B$. This gives a reasonable approximation. Pauling writes this as
\begin{equation}
|\psi\rangle =A H(R_1) H_+ (R_2)+ B H_+(R_1) H(R_2),
\end{equation}
which is interpreted as a {\em resonance} between one hydrogen being ionized, and the other being ionized.

Where things becomes interesting is if you take a molecule that has a partially ionic character to its bond -- say $HF$. There you would write:
\begin{equation}
|\psi\rangle = A H(R_1) F(R_2)+B H_+(R_1) F_-(R_2)+C H_-(R_1) F_+(R_2).
\end{equation}
An ionic bond is one where the charge distribution is concentrated towards one of the two nuclei. It turns out that the flourine more strongly binds electrons, so the $C$ term is nearly zero. The amount of ionic character can be quantified by the ratio of $B$ to $A$. Note that if you take $R_1$ sufficiently far from $R_2$ then the coefficient $B$ becomes extremely small: you never want to spontaneously ionize isolated atoms.

Excitations

Molecules have three sorts of excitations: electronic, vibrational, and rotational. The electronic excitations involve electrons moving from one orbital to another. These typically have a scale of eV. Vibrational excitations involve the relative motion of the protons. These have energies which are a fraction of an eV. Rotational excitations involve spinning. They have energies of order $10^{-3}$eV. In your homework you will analyze these, and find these scales.