One of the great organizing principles in quantum mechanics is the idea that the symmetries of a system are reflected in the spectrum. This is used in atomic, nuclear, solid state and high energy physics. We will return to it many times. An even more crucial concept is the idea that near-symmetries lead to hierarchies in the spectra.

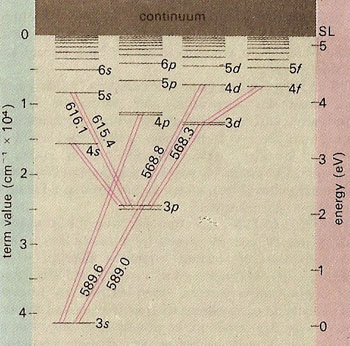
Sodium Spectrum

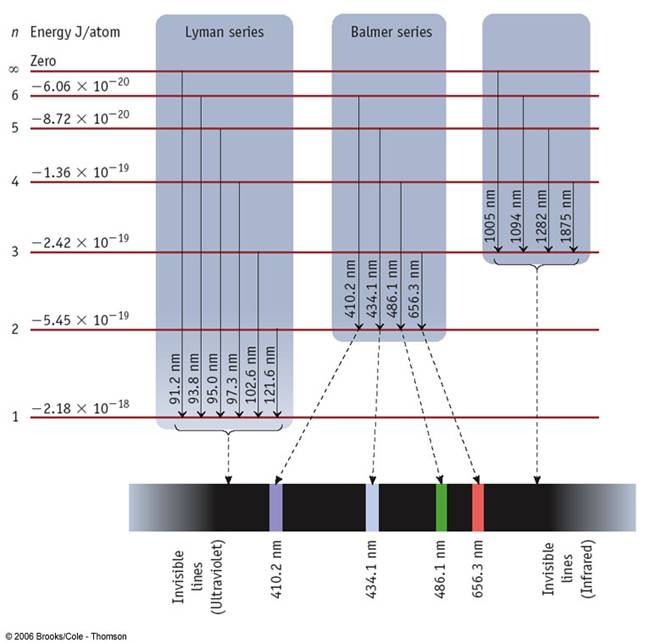
Here is a sample of the optical spectrum of Sodium, and that of Hydrogen. How do these differ?

The explanation of the differences can be explained in terms of the energy levels available to the ``valence" electron in sodium:

There are two stories we will explore today -- both of them relate to symmetries.

Hydrogen

The hydrogen spectrum is a lot more "ordered" than sodium. It has a lot of degeneracies. This is due to symmetries. Here we will explore these a bit.

As you recall, the time independent Shrodinger equation (which yields the energy eigenstates) for Hydrogen is:
\begin{equation}
\frac{-\hbar \nabla^2}{2m} \psi({\bf r}) - \frac{e^2}{4\pi \epsilon_0 r} \psi({\bf r})=E\psi({\bf r}).
\end{equation}
This is a partial differential in three variables. One typically solves it by separating variables, writing in spherical coordinates
\begin{equation}
\psi({\bf r})= f(r)g(\theta)h(\phi).
\end{equation}
You get three differential equations, each of which has an eigenvalue parameter. Thus the solution is labeled by three numbers $n,\ell,m$. By convention these are all integers, with $|m|\leq \ell\leq n$. Generically, you would expect the energy to be a function of all three of these numbers. The magic of the Hydrogen atom, is that one finds
$$
E=\frac{-E_R}{n^2},
$$
where $E_R=13.6$eV. The hydrogen atom's energy does not depend on $\ell$ or $m$. This is because of symmetries.

The independence of the energy on $m$ is due to rotational invariance: you would expect any spherically symmetric potential to yield an energy independent of $m$. We will prove this shortly. The independence from $\ell$ is more subtle, and is related to a symmetry you encountered as a Freshman, but was never explicitly pointed out to you. You probably remember Kepler's laws of planetary motion:

1. The orbit of every planet is an ellipse with the Sun at one of the two foci.
2. A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.
3. The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.

The second law is nothing but conservation of angular momentum: and is equivalent to the quantum mechanical statement that the energy is independent of $m$. The first law, however is quite unexpected. Consider what you would expect trajectories to look like for a generic central potential:


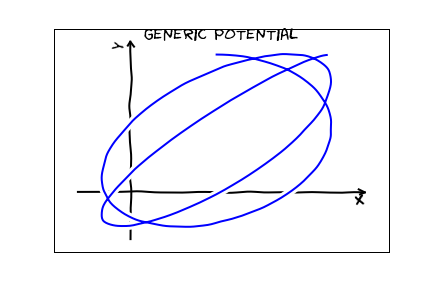
For a coulomb potential, the classical trajectories are special: they are all closed. One can associate this remarkable result with a symmetry. It is a pretty abstract symmetry. You may study this symmetry in an advanced classical mechanics class -- it is associated with a conserved quantity, the Lenz vector. It is a bit too abstract and mathematical for this course though. In quantum mechanics, this same symmetry makes the energy independent of $\ell$.

Independence of energy on $m$

There are a few ways to show that spherical symmetry gives a spectrum which is independent of $m$. In PHYS 3316 you saw at least one of these ways. Here is a review of that argument. It is a bit abstract -- but that abstraction is what makes it generalizable.

The starting point is the components of angular momentum
\begin{eqnarray}
L_z&=&x p_y-y p_x\\
L_x&=&y p_z-z p_y\\
L_y&=&z p_x-x p_z.
\end{eqnarray}
These obey commutation relations
\begin{equation}
[L_x,L_y]= i L_z,
\end{equation}
and its cyclical permutations,
\begin{eqnarray}
\,[L_y,L_z]&=& i L_x,\\
\,[L_z,L_x]&=& i L_y,
\end{eqnarray}
I assume you derived these in PHYS 3316. If not, it is a pretty easy calculation: just write it out. An algebra like this with three elements is a bit of a pain. We can make life simpler by taking linear combinations of the last two equations to give:
\begin{equation}
[L_x\pm i L_y,L_z]=\mp (L_x\pm i L_y).
\end{equation}
This is great, because it means that $L_\pm=L_x\pm i L_y$ are ``Ladder operators". That is, suppose that we have an eigenstate of $L_z$ with quantum number $m$:
\begin{equation}
(L_z \psi)({\bf r})= m \psi({\bf r}).
\end{equation}
Then $\psi_\pm=L_\pm \psi$ is an eigenstate of $L_z$ with quantum number $m\pm 1$. To see this, one first notes
\begin{equation}
L_z \psi_+ = L_z L_+ \psi.\end{equation}
One then uses the commutation relations to write this as
\begin{equation}
\qquad\qquad\qquad =L_+ (L_z+1) \psi
\end{equation}
One then uses that $\psi$ is an eigenstate of $L_z$ to reduce this to
\begin{equation}
\qquad\qquad\qquad = (m+1) L_+ \psi.
\end{equation}
Finally, one recognizes the state as $\psi_+$, i.e.
\begin{equation}
\qquad\qquad\qquad = (m+1) \psi_+.
\end{equation}

The real magic is that if we assume that $\psi$ is an eigenstate of $H$, and that $[L_\pm,H]=0$, then essentially the same argument will give that $\psi_\pm$ is also an eigenstate of $H$, with the same energy.

Fine Structure

So the Lenz vector story explains why the different angular momenta have the same energy in Hydrogen.
But what is up with that split line in sodium?

I feel a bit guilty about spending so long on the Lenz vector, because this splitting has nothing to do with that: Both of those levels have $\ell=1$. [Later we will see that you can tell they are L=1 by looking at the intensity.] The physics here has to do with the fact an electron has spin.

Recall, an electron has a magnetic moment $\mu_e$ of scale $10^{-23}$J/T ($=e\hbar/2m_e$). There is a near-symmetry, in that the energy is almost independent of the direction of this spin. The almost is quite subtle -- it is because of special relativity. This effect is known as ``fine structure coupling." In fact, Hydrogen also has fine-structure splitting, but it is very small, and hard to resolve.

Lamb Shift

There is one more important thing to mention: the 2s and 2p levels in Hydrogen are split by a subtle effect -- the Lamb shift. This effect comes from including the dynamics of the electromagnetic field (something we have left out of the Schrodinger equation). One often thinks about it as the fact that the electron is "dressed" by virtual photons, and is therefore fuzzy. The Lamb shift was a Nobel prize winning discovery, and was instrumental in demonstrating the quantum nature of photons. It is, however, a really tiny effect.