There is a simple step from the discussion of Hydrogen atoms on Thursday to a full explanation of the entire periodic table. I apologize if you have already heard this story (some of it is highschool chemistry), but it is so beautiful, that it is worth hearing a second time. Moreover I believe that with your knowledge of quantum mechanics, we can make the discussion pretty deep. (Certainly much deeper than highschool chemistry.) Here we are not so focussed on the rules and notation, but rather on the logic behind them.
Our goal is to understand many-electron atoms. Our starting point is to imagine we are an electron in a high $Z$ atom ($Z$ is the charge of the nucleus). We see some sort of combined potential from the nucleus, and all the other $Z-1$ electrons. Formally we can use a variational wavefunction to build this up.
If we are far away from the nucleus, we can imagine that all of these electrons and the nucleus are at one point, and we will see something like the coulomb potential of a point particle with charge $e$. This is referred to as ``screening". If we are very close, we see the bare nucleus, and hence a potential from a point particle with charge $Z e$. The resulting potential should look something like this:
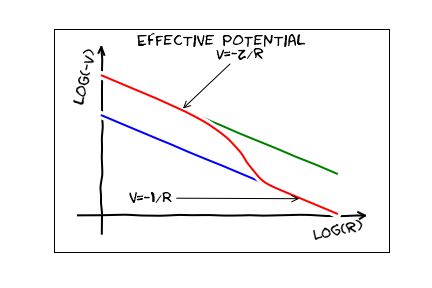
The eigenstates here will look pretty similar to the hydrogen eigenstates, but since this has fewer symmetries, the energy will depend on both $n$ and $\ell$. To make use of this, we need one more axiom of quantum mechanics, the Pauli exclusion principle. Pauli says that you cannot put more than one electron in any given quantum state. We saw this last day when we talked about quantum statistics. Consequently, both the orbital state (specified by $n,\ell,m$) and the spin state (specified by another quantum number $s=\pm1/2$). A crude model of a multielectron atom is to just fill up the hydrogenic levels one at a time. This is exactly the Hartree-Fock approximation mentioned last day. The simplest way to model this situation is with the "Hartree" approximation. Hartree is a poor man's version of Hartree-Fock. To do Hartree-Fock, you would write down a variational wavefunction, which is an antisymmetric combination of single particle wavefunctions. You would then minimize the energy, treating the single particle wavefunctions as variational parameters. The Hartree approximation "cheats" a little bit. One recognizes that Fermionic statistics requires you to put each electron in its own orbital, but you don't antisymmetrize the wavefunction. Thus one writes the electron wavefunction as \begin{equation}\label{hartree} \psi(r_1,r_2,\cdots,r_n)=\phi_1(r_1)\phi_2(r_2)\cdots \phi_n(r_n). \end{equation} If the $\phi_j$ are normalized, then so is $\psi$. The Hamiltonian is \begin{equation} H=\sum_j \left[-\frac{\hbar^2}{2m}\nabla_j^2 - \frac{Z e^2}{4\pi \epsilon_0} \frac{1}{r_j}\right] + \sum_{i < j} \frac{e^2}{4\pi\epsilon_0} \frac{1}{|r_i-r_j|}. \end{equation} Using Eq. (\ref{hartree}) as a variational wavefunction, we would write \begin{equation} E=\langle H\rangle= \int d^3r_1\,d^3r_2\cdots d^3 r_N \psi^* H \psi. \end{equation} This looks like a pretty scary $3N$-dimensional integral. We can do it though, because $\psi$ factors. [We can also do the integrals for Hartree-Fock, by writing it as a sum of terms which factor.] Lets look, for example at one term in the kinetic energy integral \begin{equation} T_1 = \int d^3r_1\,d^3r_2\cdots d^3 r_N \psi^* \left(-\frac{\hbar^2}{2m} \nabla_1^2\right) \psi. \end{equation} By grouping terms, we can write this as \begin{equation} T_1 = \int d^3r_1\,\phi_1^*(r_1)\left(-\frac{\hbar^2}{2m} \nabla_1^2\right) \phi_1(r_1) \int d^3r_2 \phi_2^*(r_2)\phi_2(r_2)\cdots \int d^3 r_N \phi_N(r_N)^*\phi_N(R_N). \end{equation} All of these integrals are equal to unity, except for the first one. Thus \begin{equation} T_1 = \int d^3r_1\,\phi_1^*(r_1)\left(-\frac{\hbar^2}{2m} \nabla_1^2\right) \phi_1(r_1). \end{equation} Each of the terms in the kinetic energy are like this, and the total kinetic energy is \begin{equation} T=\sum_j \int d^3r\,\phi_j^*(r) \left(-\frac{\hbar^2}{2m} \nabla^2\right) \phi_j(r). \end{equation} Similarly, the interaction with the nucleus becomes \begin{equation} V_{en}=\sum_j \int d^3r\,\phi_j^*(r) \left(-\frac{Z e^2}{4\pi\epsilon_0} \frac{1}{|r|}\right) \phi_j(r). \end{equation} The electron electron interactions is also a sum of terms. Lets look at one of them \begin{equation} V_{12}= \frac{e^2}{4\pi\epsilon_0} \left\langle \frac{1}{|r_1-r_2|}\right\rangle. \end{equation} The expectation value is an integral \begin{equation} \left\langle \frac{1}{|r_1-r_2|}\right\rangle= \int d^3r_1\,d^3r_2\cdots d^3 r_N \frac{1}{|r_1-r_2|}|\phi_1(r_1)|^2|\phi_2(r_2)|^2 \cdots |\phi_N(r_N)|^2. \end{equation} The integrals over $r_3,r_4,\cdots r_N$ are trivial, leaving \begin{equation} \left\langle \frac{1}{|r_1-r_2|}\right\rangle= \int d^3r_1\,d^3r_2\cdots d^3 r_N \frac{1}{|r_1-r_2|}|\phi_1(r_1)|^2|\phi_2(r_2)|^2. \end{equation} Putting everything together, our variational energy is \begin{equation} E_{\rm var}=\sum_j \int d^3r\,\phi_j^*(r)\left(-\frac{\hbar^2}{2m} \nabla^2-\frac{Z e^2}{4\pi\epsilon_0} \frac{1}{|r|}\right)\phi_j(r) + \frac{ e^2}{4\pi\epsilon_0}\sum_{i < j} \int d^3r_1\,d^3r_2 \frac{1}{|r_1-r_2|}|\phi_i(r_1)|^2|\phi_j(r_2)|^2. \end{equation} This is actually a bit more sophisticated than what is usually called the "Hartree" approximation. If we have a lot of electrons, we can replace the sum $i < j$ with an unrestricted sum over $i$ and $j$, \begin{equation}\label{hartree2} E_H=\sum_j \int d^3r\,\phi_j^*(r) \left( -\frac{\hbar^2}{2m} \nabla^2 -\frac{Z e^2}{4\pi\epsilon_0} \frac{1}{|r|} \right)\phi_j(r) + \frac{1}{2} \frac{ e^2}{4\pi\epsilon_0} \int d^3r_1\,d^3r_2 \frac{1}{|r_1-r_2|} \left(\sum_i |\phi_i(r_1)|^2\right) \left(\sum_j |\phi_j(r_2)|^2\right). \end{equation} This form is nice because the last term is nice because if we think about the electrons as a fluid (just as we thought about the atomic gas in early lectures) its density can be thought of as \begin{equation} \rho(r) =\sum_j |\phi_j(r)|^2. \end{equation} The Hartree form of the interaction is just the Coulomb energy of a classical fluid with this density Our final step is to minimize Eq. (\ref{hartree2}. We know that if we minimized just the first part (with the normalization constraint), we would get the Schrodinger equation: \begin{equation} E_j \phi_j(r)= \left(-\frac{\hbar^2}{2m} \nabla^2-\frac{Z e^2}{4\pi\epsilon_0} \frac{1}{|r|}\right)\phi_j(r). \end{equation} Adding the interaction gives \begin{equation} E_j \phi_j(r)= \left(-\frac{\hbar^2}{2m} \nabla^2+ V_{\rm eff}(r)\right)\phi_j(r), \end{equation} where \begin{equation} V_{\rm eff}(r) =\frac{Z e^2}{4\pi\epsilon_0} \frac{1}{|r|} +\int dr^\prime\, \frac{ e^2}{4\pi\epsilon_0} \frac{1}{|r-r^\prime|} \rho(r^\prime). \end{equation} Within the Hartree approximation, the energy of the electronic state is \begin{equation} E=\sum_{j=1}^Z E_j \end{equation} where $E_j$ are the eigenstates of the effective potential. It turns out that we can always choose $V_{\rm eff}$ so that it is a radial potential, only depending on $|r|$. As with hydrogen, the eigenstates can then be labeled by three quantum numbers $n,\ell,m$, corresponding to the number of nodes, the angular momentum, and the projection of the angular momentum along the $\hat z$ axis. As with any spherically symmetric potential, the energy will not depend on $m$, which will run over integers satisfying $-\ell \leq m \leq \ell$. The energy will depend on $n$ and $\ell$, with $0 \leq \ell < n$ and $n\geq 1$. We also add spin, which in this context means we can put two electrons in each single particle orbital. Traditionally one assigns various lower case letters to $\ell$. In particular, one takes $\ell=0,1,2,3,4,\cdots$ to be $s,p,d,f,g,h,i,k,l,m,\cdots$. I have never needed to go beyond $g$, and I am an atomic physicist -- but after that they are just alphabetical (there is no $j$). Historically, these letters came from the properties of the spectral lines of alkali atoms. For example transitions from atomic $s$ levels are very "sharp". The dominant lines in alkali come from $\ell=1$ states, so these got the name ``principle". Transitions with $d$ electrons are ``diffuse". Finally, for some reason that seemed good at the time, transitions with $f$ electrons were described as ``fundamental". The rest are just alphabetical. One typically combines information about $\ell$ and $n$, and writes $1s$ for the $n=1, \ell=0$ state, or $6p$ for the $n=6,\ell=1$ state. One can then say what all the electrons in an atom are doing by writing something like: $1s^22s^22p^6$ which says that there are two electrons in $1s$ states, two in $2s$ states, and $6$ in $2p$ states. Now we are ready to discuss the periodic table. As you know, the periodic table is a list of all of the elements. The remarkable feature is that the chemical properties of the elements are ``periodic": Hydrogen, Lithium, Sodium, Potassium, and Francium, all have very similar properties. The physical basis of this has to do with the fact that the outermost electrons are responsible for most of chemistry. Thus all atoms with a single s-electron in their outermost shell, will be chemically similar. Empirically, filling goes more-or-less in the following order: $1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p$. This is more a rule-of-thumb than a solid fact. In particular, most of the transition metals have funky orderings of the levels -- this makes them chemically interesting. Note, this notation is what you use when you talk about optical spectroscopy. In Xray studies you often use letters for the principle quantum number $n$. The $n=1$ states form the $K$ shell. The $n=2$ from the $L$ shell, and so on alphabetically. When you have more than one electron in the highest level, our notation does not unambiguously describe what they are doing. Take for example $2p^3$. There are $6$ possible $2p$ states -- but only 3 electrons in them. There is another set of notation for organizing them, but to understand the notation, we have to build up a bit more understanding of how to think about wavefunctions with spin. The rule of thumb that you probably learned in highschool is "Hund's Rules." They say that you want to try to line up as many of the electron spins as you can, and maximize the electronic angular momentum. Last year I had a homework problem where the students proved this. Everyone thought it was too tedious, so I will not give it this year. I will however say that using the variational principle, you have the tools to show this.

The eigenstates here will look pretty similar to the hydrogen eigenstates, but since this has fewer symmetries, the energy will depend on both $n$ and $\ell$. To make use of this, we need one more axiom of quantum mechanics, the Pauli exclusion principle. Pauli says that you cannot put more than one electron in any given quantum state. We saw this last day when we talked about quantum statistics. Consequently, both the orbital state (specified by $n,\ell,m$) and the spin state (specified by another quantum number $s=\pm1/2$). A crude model of a multielectron atom is to just fill up the hydrogenic levels one at a time. This is exactly the Hartree-Fock approximation mentioned last day. The simplest way to model this situation is with the "Hartree" approximation. Hartree is a poor man's version of Hartree-Fock. To do Hartree-Fock, you would write down a variational wavefunction, which is an antisymmetric combination of single particle wavefunctions. You would then minimize the energy, treating the single particle wavefunctions as variational parameters. The Hartree approximation "cheats" a little bit. One recognizes that Fermionic statistics requires you to put each electron in its own orbital, but you don't antisymmetrize the wavefunction. Thus one writes the electron wavefunction as \begin{equation}\label{hartree} \psi(r_1,r_2,\cdots,r_n)=\phi_1(r_1)\phi_2(r_2)\cdots \phi_n(r_n). \end{equation} If the $\phi_j$ are normalized, then so is $\psi$. The Hamiltonian is \begin{equation} H=\sum_j \left[-\frac{\hbar^2}{2m}\nabla_j^2 - \frac{Z e^2}{4\pi \epsilon_0} \frac{1}{r_j}\right] + \sum_{i < j} \frac{e^2}{4\pi\epsilon_0} \frac{1}{|r_i-r_j|}. \end{equation} Using Eq. (\ref{hartree}) as a variational wavefunction, we would write \begin{equation} E=\langle H\rangle= \int d^3r_1\,d^3r_2\cdots d^3 r_N \psi^* H \psi. \end{equation} This looks like a pretty scary $3N$-dimensional integral. We can do it though, because $\psi$ factors. [We can also do the integrals for Hartree-Fock, by writing it as a sum of terms which factor.] Lets look, for example at one term in the kinetic energy integral \begin{equation} T_1 = \int d^3r_1\,d^3r_2\cdots d^3 r_N \psi^* \left(-\frac{\hbar^2}{2m} \nabla_1^2\right) \psi. \end{equation} By grouping terms, we can write this as \begin{equation} T_1 = \int d^3r_1\,\phi_1^*(r_1)\left(-\frac{\hbar^2}{2m} \nabla_1^2\right) \phi_1(r_1) \int d^3r_2 \phi_2^*(r_2)\phi_2(r_2)\cdots \int d^3 r_N \phi_N(r_N)^*\phi_N(R_N). \end{equation} All of these integrals are equal to unity, except for the first one. Thus \begin{equation} T_1 = \int d^3r_1\,\phi_1^*(r_1)\left(-\frac{\hbar^2}{2m} \nabla_1^2\right) \phi_1(r_1). \end{equation} Each of the terms in the kinetic energy are like this, and the total kinetic energy is \begin{equation} T=\sum_j \int d^3r\,\phi_j^*(r) \left(-\frac{\hbar^2}{2m} \nabla^2\right) \phi_j(r). \end{equation} Similarly, the interaction with the nucleus becomes \begin{equation} V_{en}=\sum_j \int d^3r\,\phi_j^*(r) \left(-\frac{Z e^2}{4\pi\epsilon_0} \frac{1}{|r|}\right) \phi_j(r). \end{equation} The electron electron interactions is also a sum of terms. Lets look at one of them \begin{equation} V_{12}= \frac{e^2}{4\pi\epsilon_0} \left\langle \frac{1}{|r_1-r_2|}\right\rangle. \end{equation} The expectation value is an integral \begin{equation} \left\langle \frac{1}{|r_1-r_2|}\right\rangle= \int d^3r_1\,d^3r_2\cdots d^3 r_N \frac{1}{|r_1-r_2|}|\phi_1(r_1)|^2|\phi_2(r_2)|^2 \cdots |\phi_N(r_N)|^2. \end{equation} The integrals over $r_3,r_4,\cdots r_N$ are trivial, leaving \begin{equation} \left\langle \frac{1}{|r_1-r_2|}\right\rangle= \int d^3r_1\,d^3r_2\cdots d^3 r_N \frac{1}{|r_1-r_2|}|\phi_1(r_1)|^2|\phi_2(r_2)|^2. \end{equation} Putting everything together, our variational energy is \begin{equation} E_{\rm var}=\sum_j \int d^3r\,\phi_j^*(r)\left(-\frac{\hbar^2}{2m} \nabla^2-\frac{Z e^2}{4\pi\epsilon_0} \frac{1}{|r|}\right)\phi_j(r) + \frac{ e^2}{4\pi\epsilon_0}\sum_{i < j} \int d^3r_1\,d^3r_2 \frac{1}{|r_1-r_2|}|\phi_i(r_1)|^2|\phi_j(r_2)|^2. \end{equation} This is actually a bit more sophisticated than what is usually called the "Hartree" approximation. If we have a lot of electrons, we can replace the sum $i < j$ with an unrestricted sum over $i$ and $j$, \begin{equation}\label{hartree2} E_H=\sum_j \int d^3r\,\phi_j^*(r) \left( -\frac{\hbar^2}{2m} \nabla^2 -\frac{Z e^2}{4\pi\epsilon_0} \frac{1}{|r|} \right)\phi_j(r) + \frac{1}{2} \frac{ e^2}{4\pi\epsilon_0} \int d^3r_1\,d^3r_2 \frac{1}{|r_1-r_2|} \left(\sum_i |\phi_i(r_1)|^2\right) \left(\sum_j |\phi_j(r_2)|^2\right). \end{equation} This form is nice because the last term is nice because if we think about the electrons as a fluid (just as we thought about the atomic gas in early lectures) its density can be thought of as \begin{equation} \rho(r) =\sum_j |\phi_j(r)|^2. \end{equation} The Hartree form of the interaction is just the Coulomb energy of a classical fluid with this density Our final step is to minimize Eq. (\ref{hartree2}. We know that if we minimized just the first part (with the normalization constraint), we would get the Schrodinger equation: \begin{equation} E_j \phi_j(r)= \left(-\frac{\hbar^2}{2m} \nabla^2-\frac{Z e^2}{4\pi\epsilon_0} \frac{1}{|r|}\right)\phi_j(r). \end{equation} Adding the interaction gives \begin{equation} E_j \phi_j(r)= \left(-\frac{\hbar^2}{2m} \nabla^2+ V_{\rm eff}(r)\right)\phi_j(r), \end{equation} where \begin{equation} V_{\rm eff}(r) =\frac{Z e^2}{4\pi\epsilon_0} \frac{1}{|r|} +\int dr^\prime\, \frac{ e^2}{4\pi\epsilon_0} \frac{1}{|r-r^\prime|} \rho(r^\prime). \end{equation} Within the Hartree approximation, the energy of the electronic state is \begin{equation} E=\sum_{j=1}^Z E_j \end{equation} where $E_j$ are the eigenstates of the effective potential. It turns out that we can always choose $V_{\rm eff}$ so that it is a radial potential, only depending on $|r|$. As with hydrogen, the eigenstates can then be labeled by three quantum numbers $n,\ell,m$, corresponding to the number of nodes, the angular momentum, and the projection of the angular momentum along the $\hat z$ axis. As with any spherically symmetric potential, the energy will not depend on $m$, which will run over integers satisfying $-\ell \leq m \leq \ell$. The energy will depend on $n$ and $\ell$, with $0 \leq \ell < n$ and $n\geq 1$. We also add spin, which in this context means we can put two electrons in each single particle orbital. Traditionally one assigns various lower case letters to $\ell$. In particular, one takes $\ell=0,1,2,3,4,\cdots$ to be $s,p,d,f,g,h,i,k,l,m,\cdots$. I have never needed to go beyond $g$, and I am an atomic physicist -- but after that they are just alphabetical (there is no $j$). Historically, these letters came from the properties of the spectral lines of alkali atoms. For example transitions from atomic $s$ levels are very "sharp". The dominant lines in alkali come from $\ell=1$ states, so these got the name ``principle". Transitions with $d$ electrons are ``diffuse". Finally, for some reason that seemed good at the time, transitions with $f$ electrons were described as ``fundamental". The rest are just alphabetical. One typically combines information about $\ell$ and $n$, and writes $1s$ for the $n=1, \ell=0$ state, or $6p$ for the $n=6,\ell=1$ state. One can then say what all the electrons in an atom are doing by writing something like: $1s^22s^22p^6$ which says that there are two electrons in $1s$ states, two in $2s$ states, and $6$ in $2p$ states. Now we are ready to discuss the periodic table. As you know, the periodic table is a list of all of the elements. The remarkable feature is that the chemical properties of the elements are ``periodic": Hydrogen, Lithium, Sodium, Potassium, and Francium, all have very similar properties. The physical basis of this has to do with the fact that the outermost electrons are responsible for most of chemistry. Thus all atoms with a single s-electron in their outermost shell, will be chemically similar. Empirically, filling goes more-or-less in the following order: $1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p$. This is more a rule-of-thumb than a solid fact. In particular, most of the transition metals have funky orderings of the levels -- this makes them chemically interesting. Note, this notation is what you use when you talk about optical spectroscopy. In Xray studies you often use letters for the principle quantum number $n$. The $n=1$ states form the $K$ shell. The $n=2$ from the $L$ shell, and so on alphabetically. When you have more than one electron in the highest level, our notation does not unambiguously describe what they are doing. Take for example $2p^3$. There are $6$ possible $2p$ states -- but only 3 electrons in them. There is another set of notation for organizing them, but to understand the notation, we have to build up a bit more understanding of how to think about wavefunctions with spin. The rule of thumb that you probably learned in highschool is "Hund's Rules." They say that you want to try to line up as many of the electron spins as you can, and maximize the electronic angular momentum. Last year I had a homework problem where the students proved this. Everyone thought it was too tedious, so I will not give it this year. I will however say that using the variational principle, you have the tools to show this.
